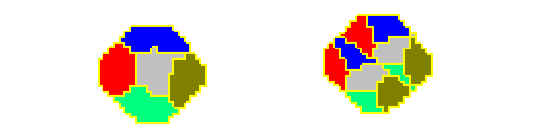Dividing cluster cells
While dividing non-clustered cells is straightforward, doing the same for clustered cells is more challenging. To divide non-cluster cell using directional mitosis algorithm we construct a line or a plane passing through center of mass of a cell and pixels of the cell (we are using PixelTracker plugin with mitosis) on one side of the line/plane end up in child cell and the rest stays in parent cell. The orientation of the line/plane can be either specified by the user or we can use CC3D built-in feature to calculate calculate orientation tion of principal axes and divide either along minor or major axis.
With compartmental cells, things get more complicated because: 1) Compartmental cells are composed of many subcells. 2) There can be different topologies of clusters. Some clusters may look “snake-like” and some might be compactly packed blobs of subcells. The algorithm which we implemented in CC3D works in the following way:
We first construct a set of pixels containing every pixel belonging to a cluster cell. You may think of it as of a single “regular” cell.
We store volumes of compartments so that we know how big compartments should be after mitosis (they will be half of original volume)
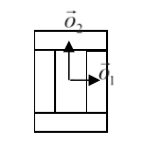
We calculate center of mass of entire cluster and calculate vector offsets between center of mass of a cluster and center of mass of particular compartments as on the figure below:
Figure 7.Vectors \(\vec{o}_1\) and \(\vec{o}_2\) show offsets between center of mass of a cluster and center of mass particular compartments.
4) We pick division line/plane and for parents and child cells with offsets between cluster center of mass (after mitosis) and center of masses of clusters. We do it according to the formula:
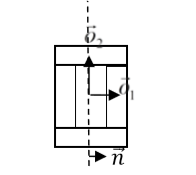
where \(\vec{p}\) denotes offset after mitosis from center of mass of child (parent) clusters, \(\vec{o}\) is orientation vector before mitosis (see picture above) and \(\vec{n}\) is a normalized vector perpendicular to division line/plane. If we try to divide the cluster along dashed line as on the picture below:
Figure 8. Division of cell along dashed line. Notice the orientation of \(\vec{n}\) . The offsets after the mitosis for child and parent cell will be \(\vec{p}_1=\frac{1}{2}\vec{o}_1\) and \(\vec{p}_2=\vec{o}_2\) as expected because both parent and child cells will retain their heights but after mitosis will become twice narrower (cell with grey outer
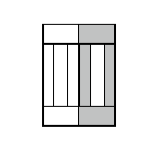
compartments is a parent cell):
Figure 9.Child and parent (the one with grey outer compartments) cells after mitosis.
The formula given above is heuristic. It gives fairly simple way of assigning pixels of child/parent clusters to cellular compartments. It is not perfect but the idea is to get approximate shape of the cell after the mitosis and as simulation runs cell shape will readjust based on constraints such as adhesion of focal point plasticity. Before continuing with the mitosis we check if center of masses of compartments belong to child/parent clusters. If the center of masses are outside their target pixels we abandon mitosis and wait for readjustment of cell shape at which point mitosis algorithm will pass this sanity check. For certain “exotic” shapes of cluster shapes presented mitosis algorithm may not work well or at all. In this case we would have to write specialized mitosis algorithm.
5) We divide clusters and knowing offsets from child/parent cluster center of mass we assign pixels to particular compartments. The assignment is based on the distance of particular pixel to center of masses of clusters. Pixel is assigned to particular compartment if its distance to the center of mass of the compartment is the smallest as compared to distances between centroids of other compartments. If given compartment has reached its target volume and other compartments are underpopulated we would assign pixels to other compartments based on the closest distance criterion. Although this method may result in some deviation from perfect 50-50 division of compartment volume in most cases after few MCS cells will readjust their volume.
Figure 10. CC3D example of compartmental cell division. See also Demos/CompuCellPythonTutorial/clusterMitosis.