Calculating center of mass when using periodic boundary conditions.
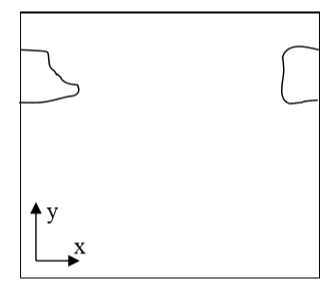
When you are running calculation with periodic boundary condition you may end up with situation like in the figure below:
Figure 6 A connected cell in the lattice edge area – periodic boundary conditions are applied
Clearly, what happens is that simply connected cell is wrapped around the lattice edge so part of it is in the region of high values of x coordinate and the other is in the region where x coordinates have low values. Consequently, a naïve calculation of center of mass position according to:
or in vector form:
would result in being somewhere in the middle of the lattice and obviously outside the cell. A better procedure could be as follows:
Before calculating center of mass when new pixel is added or lost we “shift” a cell and new pixel (gained or lost )to the middle of the lattice do calculations “in the middle of the lattice” and shift back. Now if after shifting back it turns out that center of mass of a cell lies outside lattice position it in the center of mass by applygin a shift equal to the length of the lattice and whose direction should be such that the center of mass of the cell ends up inside the lattice (there is only one such shift and it might be be equal to zero vector).
This is how we do it using mathematical formulas:
First we define shift vector \(\vec{s}\) as a vector difference between vector pointing to center of mass of the cell \(\vec{r}_{COM}\) and vector pointing to (approximately) the middle of the lattice \(\vec{c}\).
Next we shift cell to the middle of the lattice using :
where \(\vec{r'}_{COM}\) denotes center of mass position of a cell after shifting but before adding or subtracting a pixel.
Next we take into account the new pixel (either gained or lost) and calculate center of mass position (for the shifted cell):
Above we have assumed that we are adding one pixel.
Now all that we need to do is to shift back \(\vec{r'}_{COM}^{new}\) by same vector \(\vec{s}\) that brought cell to (approximately) center of the lattice:
We are almost done. We still have to check if \(\vec{r'}_{COM}^{new}\) is inside the lattice. If this is not the case we need to shift it back to the lattice but now we are allowed to use only a vector \(\vec{P}\) whose components are multiples of lattice dimensions (and we can safely restrict to +1 and -1 multiples of the lattice dimensions) . For example we may have:
where \(\vec{x}_{max}\), \(\vec{y}_{max}\), \(\vec{z}_{max}\) are dimensions of the lattice.
There is no cheating here. In the lattice with periodic boundary conditions you are allowed to shift point coordinates a vector whose components are multiples of lattice dimensions.
All we need to do is to examine new center of mass position and form suitable vector \(\vec{P}\).