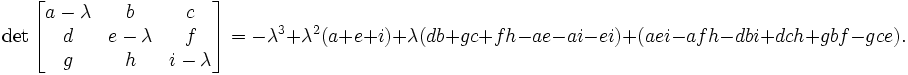Calculating shape constraint of a cell – elongation term
The shape of single cell immersed in medium and not subject to too drastic surface or surface constraints will be spherical (circular in 2D). However in certain situation we may want to use cells which are elongated along one of their body axes. To facilitate this we can place constraint on principal lengths of cell. In 2D it is sufficient to constrain one of the principal lengths of cell how ever in 3D we need to constrain 2 out of 3 principal lengths. Our first task is to diagonalize inertia tensor (i.e. find a coordinate frame transformation which brings inertia tensor to a diagonal form)
Diagonalizing inertia tensor
We will consider here more difficult 3D case. The 2D case is described in detail in M.Zajac, G.L.jones, J,A,Glazier “Simulating convergent extension by way of anisotropic differential adhesion” Journal of Theoretical Biology 222 (2003) 247–259.
In order to diagonalize inertia tensor we need to solve eigenvalue equation:
or in full form
The eigenvalue equation will be in the form of 3rd order polynomial. The roots of it are guaranteed to be real. The polynomial itself can be found either by explicit derivation, using symbolic calculation or simply in Wikipedia ( http://en.wikipedia.org/wiki/Eigenvalue_algorithm )
so in our case the eigenvalue equation takes the form:
This equation can be solved analytically, again we may use Wikipedia ( http://en.wikipedia.org/wiki/Cubic_function )
Now, the eigenvalues found that way are principal moments of inertia of a cell. That is they are components of inertia tensor in a coordinate frame rotated in such a way that off-diagonal elements of inertia tensor are 0:
In our cell shape constraint we will want to obtain ellipsoidal cells. Therefore the target tensor of inertia for the cell should be tensor if inertia for ellipsoid:
where a, b, c are parameters describing the surface of an ellipsoid:
In other words a, b, c are half lengths of principal axes (they are
analogues of circle’s radius).
Now we can determine semi axes lengths in terms of principal moments of inertia by inverting the following set of equations:
Once we have calculated semiaxes lengths in terms of moments of inertia we can plug –in actual numbers for moment of inertia (the ones for actual cell) and obtain lengths of semiexes. Next we apply quadratic constraint on largest (semimajor) and smallest (seminimor axes). This is what elongation plugin does.